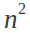Floyd Warshall ( min graph distance )

In today post i will present my result of the Aparapi GPU parallel version of the classical Floyd Warshall min graph distance. We will test on 3 complete graphs with 1024, 2048 and 4096 nodes.
 The coding of the parallel  version was very easy because the algorithm is data parallel by its nature, so what i have done was just to execute the 2 inner loop in a kernel N times ( N=number of nodes ).
 We will compare the classical iterative version and the Aparapi OpenCL version executed on the CPU and GPU. Lets see the results.

For a graph with 1024 notes ( this algorithm has a N^3 complexity so 1024 is a pretty large number )


The first thing that i noticed is that the iterative version is very fast, in total there are 1073741824 iterations to be done and the iterative version finished in 1406 ms, this means 763685 iterations per ms. Taking into account that just starting a kernel ( without memory copy or OpenCL translation ) takes around 0.6 ms on my system i think that running a kernel for performing anything less that 500 000 will run slower that an iterative version ( this number clearly differs from one system to another, but i think is in this range ).
Because of this the speed increase for the GPU version is just 2X.
One strange thing is the very bad performance for the Aparapi CPU version, I' am not sure what is causing this, i currently assume that is has to do with the algorithm not being very cache friendly when run on the CPU.

 
The gap has increased to 6.6X between the iterative version and the Aparapi version.

Another speed increase of around 10x.

Conclusions

This test proved that even if we need to run the same kernel multiple times we can still get a very good speed increase ( 10X ) the only condition is that when we start a kernel we need to have a lot of data to process, i would say at least a couple of millions operations for a marginal speed increase and around billions for a really big increase in performance.

• Results

• Java code

Levenshtein distance

 In this test i tried to adapt the classic Levenshtein_distance algorithm to Aparapi. What i have did was to basically calculate in parallel the values for each color.
 Lest say:
    A = the first string,
    B = the second string
then my algorithm runs the same kernel N = ( len(A)+len(B)-1) times  ( this number is equals with the number of different colors ). 

 

I executed the algorithm on some random generated string and here are the results:



 The GPU time is  37X slower than the iterative version for the 1024*4 length strings and 14X slower for the 1024*14 length string. Why is this?
 I did some testing and the 2 most probably caused are:
    a) Kernel start time, if you run the same kernel multiple times even if it doesn't do nothing it takes around 0.6 ms when run in GPU mode and 0.125 ms when run in CPU mode ( the 2 times are without buffer copy and java to opencl code translation ).
   b) Low number of operations executed by each kernel run. The maximum number of operations executed at on time is len(B).

 What did i learned from this? When you start a kernel make sure it has a lot of data to process at least millions if not billions of operations. If you start a kernel to make 10 000, 100 000 even 1 000 000 if will be slower than running that code on the CPU.

 Results
 Java code

Large prime calculator

 Today we will test how fast we can check if a large number ( 19 digit ) is prime. I written  a classical sequential algorithm  and an Aparapi parallel version and here are the results:



 There is a massive 50X improvement over the  sequential algorithm and a very good 14X improvement over the parallel version run on CPU. I don't know why we didn't see the same 40X improvement like in the previous 2 algorithm but 14X is still very good.
 The sequential version just checks each number for 3 to sqrt(n) if it divides n.
 The parallel version splits the interval [3, sqrt(n)] in 128*1028 equal intervals and the number from each interval are checked by a " GPU thread " ( I'am not sure what is the right terminology for this ).
 Probably you wonder why 128*1028 intervals? I tested with different number of interval and this offered the best performance, this is probably caused by the fact the GPU is very efficient in switching between and allocating resources to threads and a larger number of threads will  maximize the resource utilization ( this is just my empirical explanation ) 

Results ( spreadsheet ) and Java code

What does 40x mean?

 So you created your algorithm, tested and you got least say a 40x improvement ( like i did :).  What does this mean? How much more data you can process in the same amount of time?

 The answer of this questions is related with the complexity of your algorithm. Least say you have a O(n^2) edit distance algorithm and you can compare 2 string of length 1000 in about 1 second using your CPU and 40 times faster using your GPU, the question is what is the length of the string that you can process in 1 second using your CPU?

 The answer to this question it turns our to be rather simple:

more precisely 6324. So basically you will be able to process strings 6 times bigger in the same amount of time.

 How i calculated this? i will let you figure it out :). As a help you can use the following speed gain table.

Algorithm complexity	Speed gain ( D = speedup factor )

Matrix multiplication

Today i tested matrix multiplication using Aparapi and my 7770 card. The results are great, another 40X improvement over my quad core 960T cpu.


The interesting part is that the shape of the graphs is the same. This means that we can't change the complexity of the algorithm by using a gpu but only make it a lot run faster.

The results 

and also the Java Code

 import java.util.Random;  
 import com.amd.aparapi.Kernel;  
 public class MatrixMultiplication {  
   public static void main ( String [] arg ){  
     test( 500,500,500 );   
     test( 1000,1000,1000 );   
     test( 1500,1500,1500 );   
     test( 2000,2000,2000 );   
     test( 2500,2500,2500 );   
   }  
   public static void test ( int a, int b, int c ){  
     Random rnd = new Random();   
     int [] A = new int[a*b];  
     int [] B = new int[b*c];  
     for ( int i=0; i<A.length; i++ ){  
       A[i] = rnd.nextInt( 1000 );   
     }  
     for ( int i=0; i<B.length; i++ ){  
       B[i] = rnd.nextInt( 1000 );   
     }  
     long min = Integer.MAX_VALUE;  
     for (int i = 0; i < 2; i++) {  
       long start = System.currentTimeMillis();  
       int[] rezultat = mult(A, B, a, b, c);  
       long end = System.currentTimeMillis();  
       min = Math.min( min, end - start );   
     }  
 //    printMatrix( A, a, b );   
 //    System.out.println();   
 //    printMatrix( B, b, c );   
 //    System.out.println();   
 //    printMatrix( rezultat, a, c );  
     System.out.println( "[" + a + "," + b +"]X[" + b + "," + c + "] " + min + " ms" );   
   }  
   public static void printMatrix( int [] m, int a, int b ){  
     for ( int i=0; i<a; i++ ){  
       for ( int j=0; j<b; j++ ){  
         System.out.print( m[i*b+j] + " " );   
       }  
       System.out.println();   
     }  
   }  
   public static int [] mult( final int [] A, final int [] B, final int a, final int b, final int c ) {  
     final int [] rezultat = new int [ a * c ];   
     Kernel kernel = new Kernel() {  
       @Override  
       public void run() {  
         int k = getGlobalId();  
         int linie = k/c;  
         int coloana = k%c;  
         for ( int i=0; i<b; i++ ){  
           rezultat[k] += A[ linie*b + i ] * B[ i*c + coloana ];   
         }  
       }  
     };  
     kernel.setExecutionMode( Kernel.EXECUTION_MODE.CPU );  
     kernel.execute( rezultat.length );  
     return rezultat;   
   }  
 }  

Number of divisors

 I have found this: http://code.google.com/p/aparapi/, a java library that will translate java code to OpenCL binary code ( or something like that ), and i though to take it for a spin to see what i can do with it.

 For the first test we will calculate the number of divisors for the fist N natural numbers, will test with N = {1048576, 2097152, 3145728, 4194304, 5242880    6291456, 7340032, 8388608, 9437184 }. 
The complexity of the algorithm that i have implemented is n*sqrt(n) so normally it will not scale very well with large values of N. 


But before we begin let me introduce you to my rig:
 CPU: Phenom X4 960T
 GPU: Radeon 7770 GHZ Edition

 The price of the CPU was almost identical to that of the GPU so i think this is a fair comparison to see how much more performance you can get for the same amount of money if you use a aparapi and a GPU to solve it. 

 The performance gain is from 17X for the small instances up to 41X for the largest ones. This is almost unbelievable if you take into account how easy was to modify the algorithm into an Aparapi kernel and how cheap is to buy one of this cards.

 In the next weeks i will test this technology with some other problems to see how will perform.

Below are the results and the java code i have used for this test:

Results

1:  import com.amd.aparapi.Kernel;  
2:  public class NumberOfDivisors {  
3:    public static void main(String[] arg) {  
4:      for (int k = 1; k <= 9; k++) {  
5:        long min = Long.MAX_VALUE;  
6:        for (int t = 0; t < 4; t++) {  
7:          final int[] a;  
8:          a = new int[1024 * 1024 * k];  
9:          for (int i = 0; i < a.length; i++) {  
10:            a[i] = 0;  
11:          }  
12:          Kernel kernel = new Kernel() {  
13:            @Override  
14:            public void run() {  
15:              int k = getGlobalId();  
16:              for (int i = 2; i * i <= k; i++) {  
17:                if (k % i == 0) {  
18:                  a[k]++;  
19:                }  
20:              }  
21:            }  
22:          };  
23:          kernel.setExecutionMode(Kernel.EXECUTION_MODE.JTP);  
24:          long start = System.currentTimeMillis();  
25:          kernel.execute(a.length);  
26:          long end = System.currentTimeMillis();  
27:          min = Math.min(min, end - start);  
28:          // System.out.println(end - start + " ms");  
29:        }  
30:        System.out.println(k + " " + min + ",");  
31:      }  
32:    }  
33:  }